Numerical investigation of a neural field model including dendritic processing

Authors

Avitabile, D., Lima, P., and Coombes, S.

Abstract

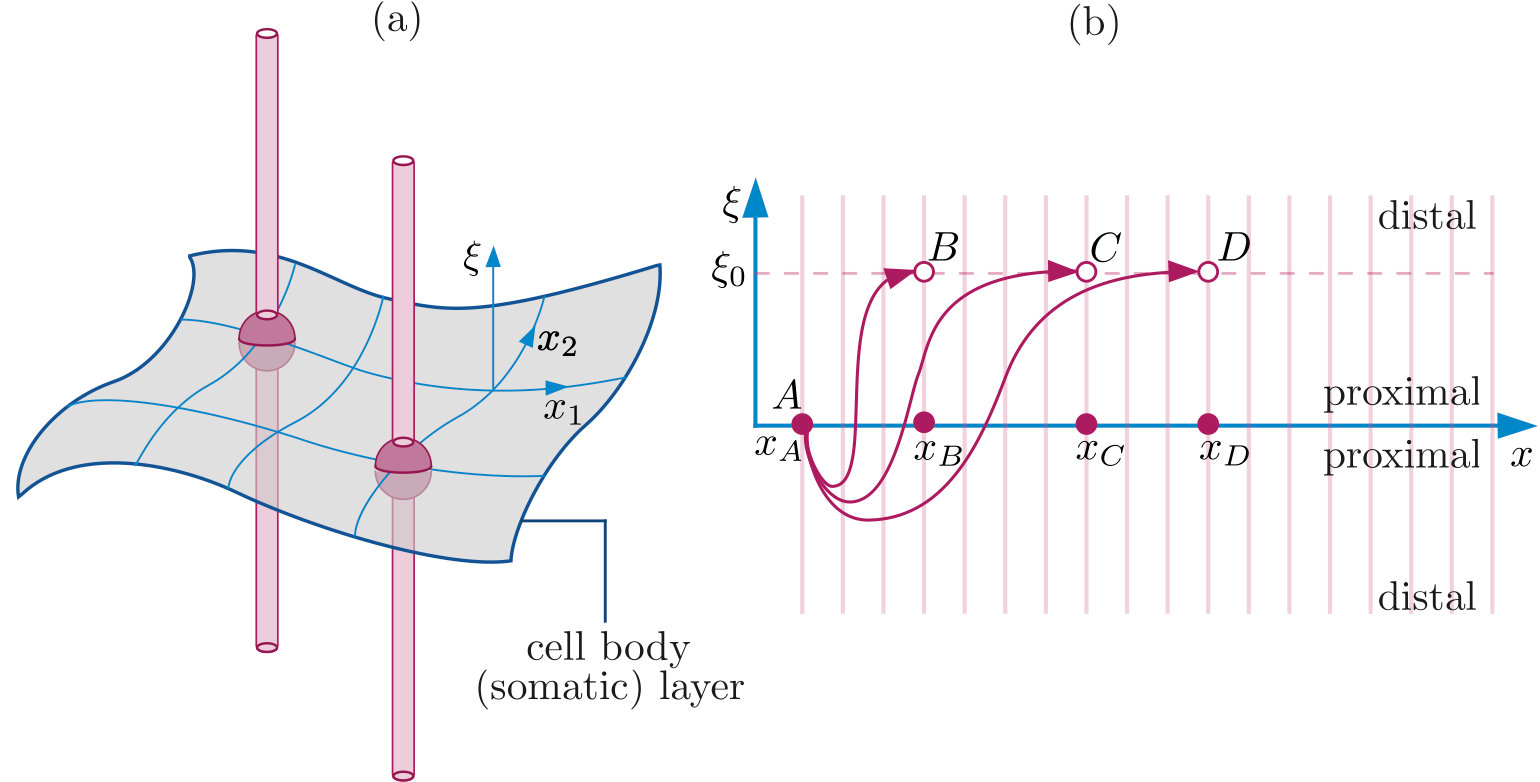
We consider a simple neural field model in which the state variable is dendritic voltage, and in which somas form a continuous one-dimensional layer. This neural field model with dendritic processing is formulated as an integro-differential equation. We introduce a computational method for approximating solutions to this nonlocal model, and use it to perform numerical simulations for neuro-biologically realistic choices of anatomical connectivity and nonlinear firing rate function. For the time discretisation we adopt an Implicit-Explicit (IMEX) scheme; the space discretisation is based on a finite-difference scheme to approximate the diffusion term and uses the trapezoidal rule to approximate integrals describing the nonlocal interactions in the model. We prove that the scheme is of first-order in time and second order in space, and can be efficiently implemented if the factorisation of a small, banded matrix is precomputed. By way of validation we compare the outputs of a numerical realisation to theoretical predictions for the onset of a Turing pattern, and to the speed and shape of a travelling front for a specific choice of Heaviside firing rate. We find that theory and numerical simulations are in excellent agreement.

Links

BibTeX

@article{avitabile2020numerical,
  title={Numerical investigation of a neural field model including dendritic processing},
  author={Avitabile, Daniele and Coombes, Stephen and Lima, Pedro M.},
  journal = {Journal of Computational Dynamics},
  volume = {7},
  number = {2158-2491_2020_2_271},
  pages = {271--290},
  year = {2020},
  doi = {10.3934/jcd.2020011}
}