Bumps and Oscillons in Networks of Spiking Neurons
Authors
Schmidt, H. and Avitabile, D.
Abstract
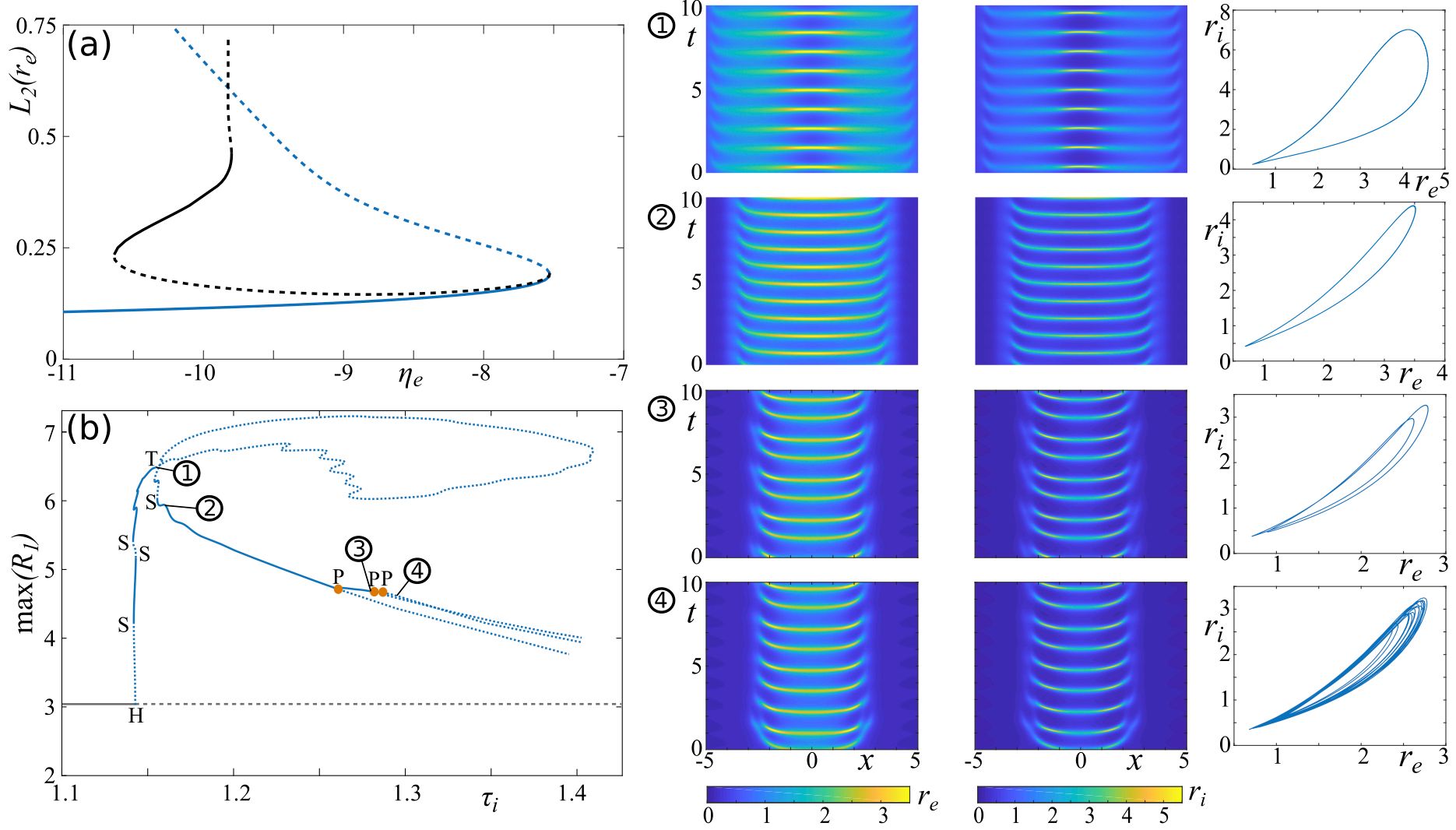
We study localized patterns in an exact mean-field description of a spatially extended network of quadratic integrate-and-fire neurons. We investigate conditions for the existence and stability of localized solutions, so-called bumps, and give an analytic estimate for the parameter range, where these solutions exist in parameter space, when one or more microscopic network parameters are varied. We develop Galerkin methods for the model equations, which enable numerical bifurcation analysis of stationary and time-periodic spatially extended solutions. We study the emergence of patterns composed of multiple bumps, which are arranged in a snake-and-ladder bifurcation structure if a homogeneous or heterogeneous synaptic kernel is suitably chosen. Furthermore, we examine time-periodic, spatially localized solutions (oscillons) in the presence of external forcing, and in autonomous, recurrently coupled excitatory and inhibitory networks. In both cases, we observe period-doubling cascades leading to chaotic oscillations.
Links
DOI ArXiv PDFBibTeX
@article{schmidt2020bumps,
author = {Schmidt, Helmut and Avitabile, Daniele},
title = {Bumps and oscillons in networks of spiking neurons},
journal = {Chaos: An Interdisciplinary Journal of Nonlinear Science},
volume = {30},
number = {3},
pages = {033133},
year = {2020},
doi = {10.1063/1.5135579},
URL = {https://doi.org/10.1063/1.5135579},
eprint = {https://doi.org/10.1063/1.5135579}
}