Continuation of localized coherent structures in nonlocal neural field equations
Authors
Rankin, J., Avitabile, D., Baladron, J., Faye, G. and Lloyd, D.J.
Abstract
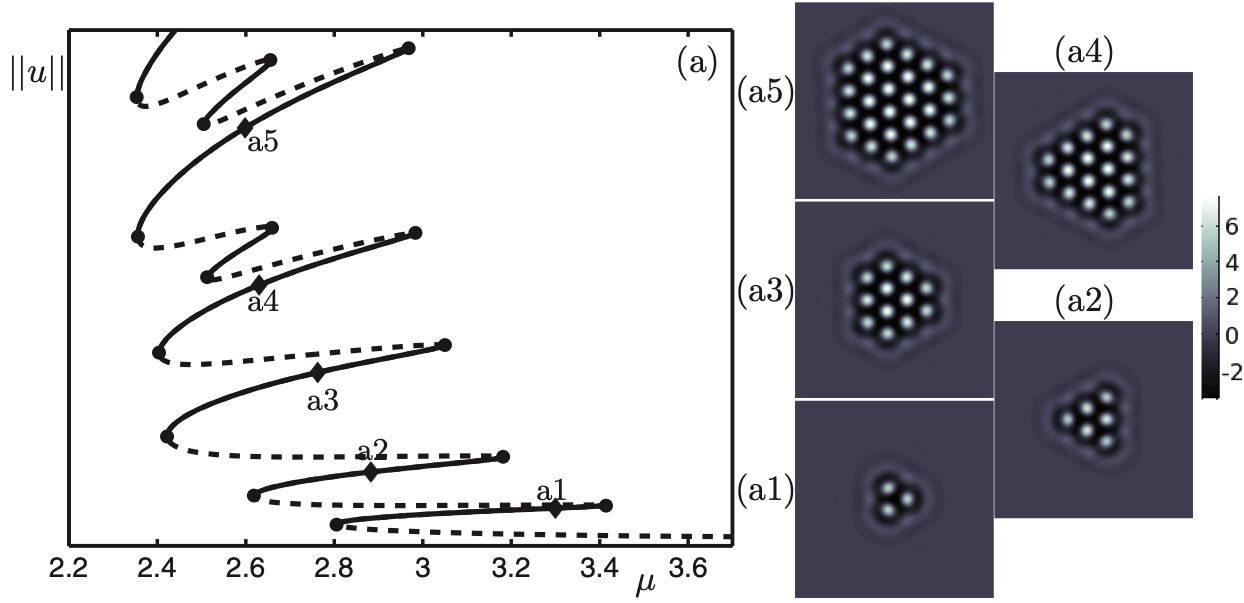
We study localized activity patterns in neural field equations posed on the Euclidean plane; such models are commonly used to describe the coarse-grained activity of large ensembles of cortical neurons in a spatially continuous way. We employ matrix-free Newton--Krylov solvers and perform numerical continuation of localized patterns directly on the integral form of the equation. This opens up the possibility of studying systems whose synaptic kernel does not lead to an equivalent PDE formulation. We present a numerical bifurcation study of localized states and show that the proposed models support patterns of activity with varying spatial extent through the mechanism of homoclinic snaking. The regular organization of these patterns is due to spatial interactions at a specific scale associated with the separation of excitation peaks in the chosen connectivity function. The results presented form a basis for the general study of localized cortical activity with inputs and, more specifically, for the investigation of the localized spread of orientation selective activity that has been observed in the primary visual cortex with local visual input.
Links
DOI arXiv PDFBibTeX
@article{rankin2014continuation,
title={Continuation of localized coherent structures in nonlocal neural field equations},
author={Rankin, James and Avitabile, Daniele and Baladron, Javier and Faye, Gregory and Lloyd, David JB},
journal={SIAM Journal on Scientific Computing},
volume={36},
number={1},
pages={B70--B93},
year={2014},
publisher={SIAM}
}