Cross-scale excitability in networks of synaptically-coupled quadratic integrate-and-fire neurons

Authors

D. Avitabile, M. Desroches, G. Bard Ermentrout

Abstract

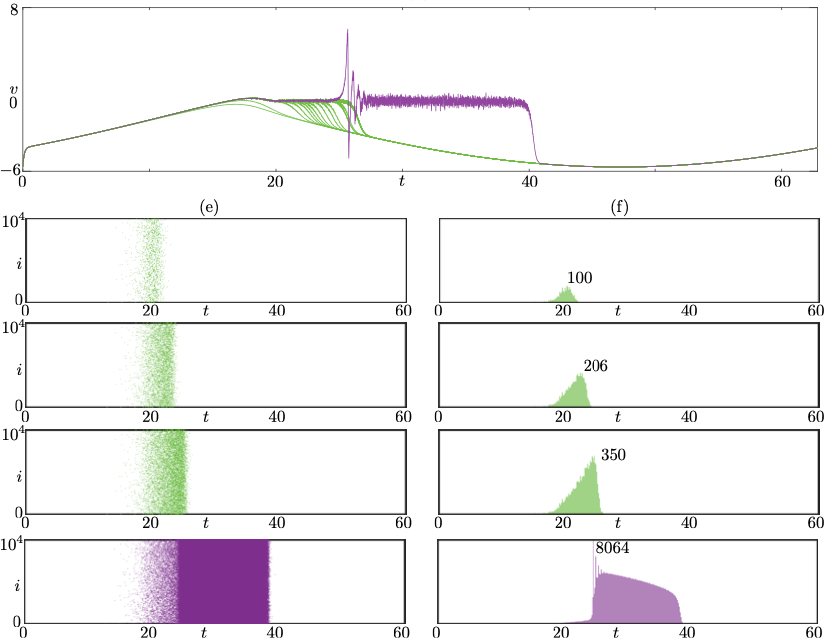
From the action potentials of neurons and cardiac cells to the amplification of calcium signals in oocytes, excitability is a hallmark of many biological signalling processes. In recent years, excitability in single cells has been related to multiple-timescale dynamics through canards, special solutions which determine the effective thresholds of the all-or-none responses. However, the emergence of excitability in large populations remains an open problem. Here, we show that the mechanism of excitability in large networks and mean-field descriptions of coupled quadratic integrate-and-fire (QIF) cells mirrors that of the individual components. We initially exploit the Ott-Antonsen ansatz to derive low-dimensional dynamics for the coupled network and use it to describe the structure of canards via slow periodic forcing. We demonstrate that the thresholds for onset and offset of population firing can be found in the same way as those of the single cell. We combine theoretical analysis and numerical computations to develop a novel and comprehensive framework for excitability in large populations, applicable not only to models amenable to Ott-Antonsen reduction, but also to networks without a closed-form mean-field limit, in particular sparse networks.

Links‌

BibTeX‌

@article{avitabile2022cross,
  title={Cross-scale excitability in networks of quadratic integrate-and-fire neurons},
  author={Avitabile, Daniele and Desroches, Mathieu and Bard Ermentrout, G},
  journal={PLoS Computational Biology},
  year={2022},
  volume={18},
  number={10},
  pages={e1010569},
  doi={e1010569},
}