Local theory for spatio-temporal canards and delayed bifurcations

Authors

Avitabile, D., Desroches, M., Veltz, R. and Wechselberger, M.

Abstract

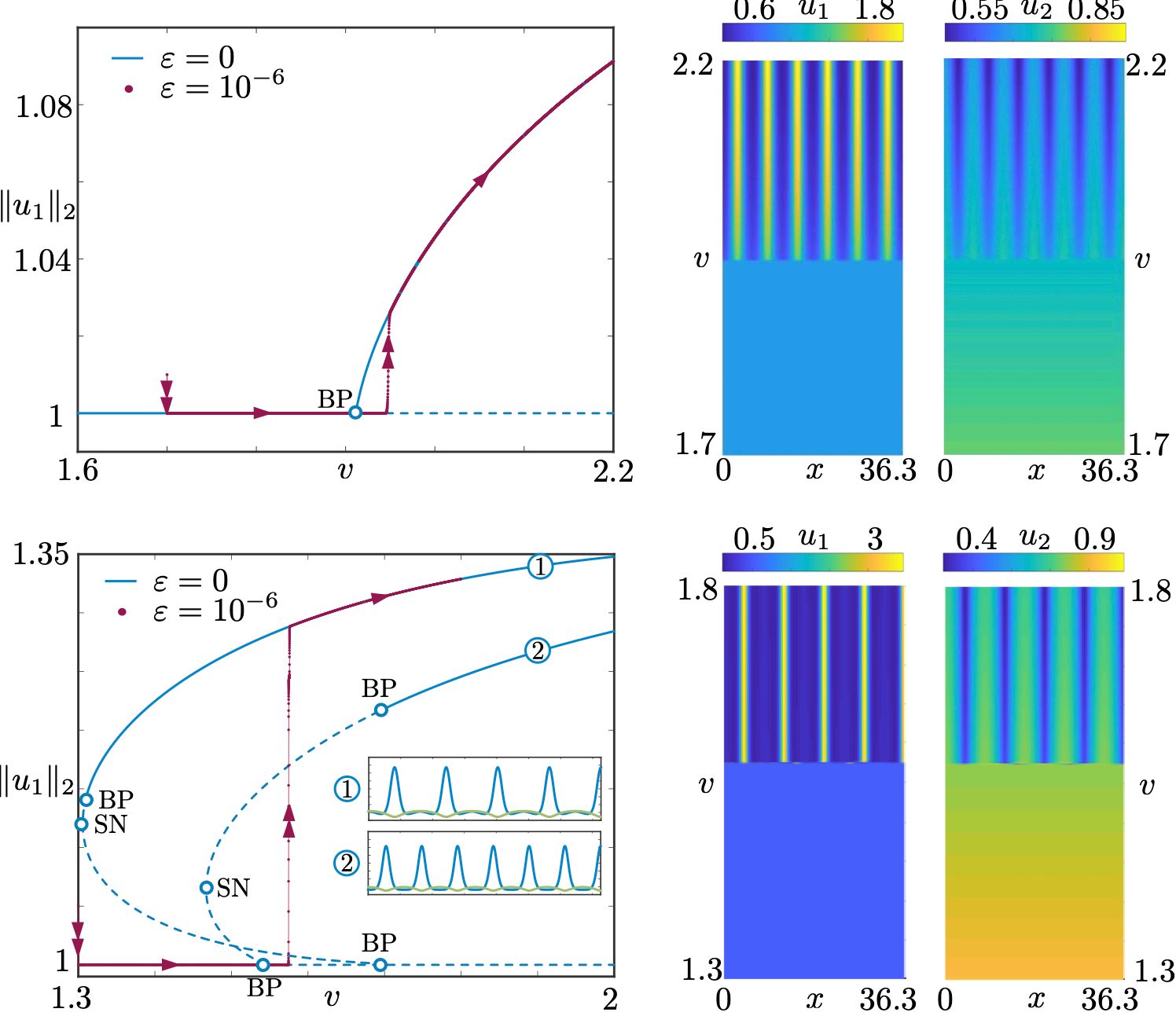
We present a rigorous framework for the local analysis of canards and slow passages through bifurcations in a wide class of infinite-dimensional dynamical systems with time-scale separation. The framework is applicable to models where an infinite-dimensional dynamical system for the fast variables is coupled to a finite-dimensional dynamical system for slow variables. We prove the existence of centre-manifolds for generic models of this type, and study the reduced, finite-dimensional dynamics near bifurcations of (possibly) patterned steady states in the layer problem. Theoretical results are complemented with detailed examples and numerical simulations covering systems of local- and nonlocal-reaction diffusion equations, neural field models, and delay-differential equations. We provide analytical foundations for numerical observations recently reported in literature, such as spatio-temporal canards and slow-passages through Hopf bifurcations in spatially-extended systems subject to slow parameter variations. We also provide a theoretical analysis of slow passage through a Turing bifurcation in local and nonlocal models.

Links

BibTeX

@article{avitabile2020local,
  title={Local theory for spatio-temporal canards and delayed bifurcations},
  author={Avitabile, Daniele and Desroches, Mathieu and Veltz, Romain and Wechselberger, Martin},
  journal={SIAM Journal on Mathematical Analysis},
  volume={52},
  number={6},
  pages={5703--5747},
  year={2020},
  publisher={SIAM}
}