Localized auxin peaks in concentration-based transport models of the shoot apical meristem
Authors
Draelants, D., Avitabile, D. and Vanroose, W.
Abstract
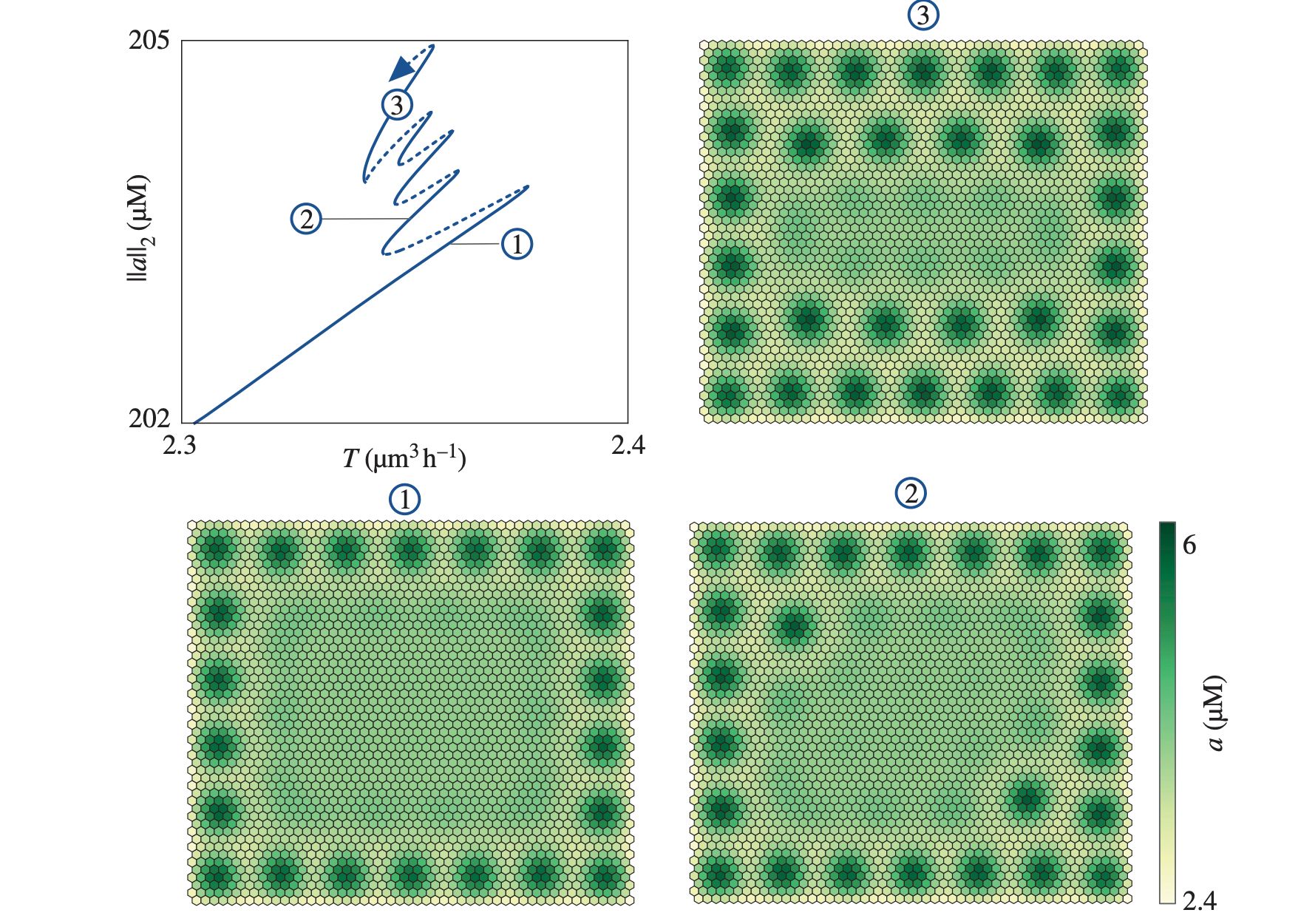
We study the formation of auxin peaks in a generic class of concentration-based auxin transport models, posed on static plant tissues. Using standard asymptotic analysis, we prove that, on bounded domains, auxin peaks are not formed via a Turing instability in the active transport parameter, but via simple corrections to the homogeneous steady state. When the active transport is small, the geometry of the tissue encodes the peaks’ amplitude and location: peaks arise where cells have fewer neighbours, that is, at the boundary of the domain. We test our theory and perform numerical bifurcation analysis on two models that are known to generate auxin patterns for biologically plausible parameter values. In the same parameter regimes, we find that realistic tissues are capable of generating a multitude of stationary patterns, with a variable number of auxin peaks, that can be selected by different initial conditions or by quasi-static changes in the active transport parameter. The competition between active transport and production rate determines whether peaks remain localized or cover the entire domain. In particular, changes in the auxin production that are fast with respect to the cellular life cycle affect the auxin peak distribution, switching from localized spots to fully patterned states. We relate the occurrence of localized patterns to a snaking bifurcation structure, which is known to arise in a wide variety of nonlinear media, but has not yet been reported in plant models.
Links
DOI arXiv PDFBibTeX
@article{draelants2015localized,
title={Localized auxin peaks in concentration-based transport models of the shoot apical meristem},
author={Draelants, Delphine and Avitabile, Daniele and Vanroose, Wim},
journal={Journal of The Royal Society Interface},
volume={12},
number={106},
pages={20141407},
year={2015},
publisher={The Royal Society}
}