Neural Fields and Noise-Induced Patterns in Neurons on Large Disordered Networks

Authors

Avitabile D., MacLaurin J.

Abstract

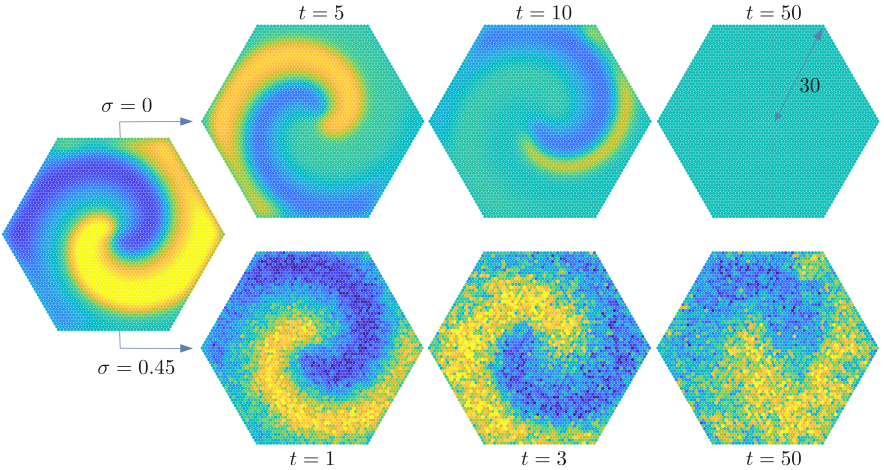
We study pattern formation in a class of high-dimensional neural networks posed on random graphs and subject to spatiotemporal stochastic forcing. Under generic conditions on coupling and nodal dynamics, we prove that the network admits a rigorous mean-field limit, resembling a Wilson–Cowan neural-field equation. The state variables of the limiting systems are the mean and variance of neuronal activity. We select networks whose mean-field equations are tractable and we perform a bifurcation analysis using as a control parameter the diffusivity strength of the afferent white noise on each neuron. We find conditions for Turing-like bifurcations in a system where the cortex is modelled as a ring, and we produce numerical evidence of noise-induced spiral waves in models with a two-dimensional cortex. We provide numerical evidence that solutions of the finite-size network converge weakly to solutions of the mean-field model. Finally, we prove a large deviation principle, which provides a means of assessing the likelihood of deviations from the mean-field equations induced by finite-size effects.

Links‌

DOI PDF Arxiv

BibTeX‌

@article{avitabile2026neural,
  author  = {Avitabile, Daniele and MacLaurin, James},
  title   = {Neural Fields and Noise-Induced Patterns in Neurons on Large Disordered Networks},
  journal = {SIAM Journal on Applied Mathematics},
  year    = {2026},
  volume  = {86},
  number  = {2},
  pages   = {427--456},
  doi     = {10.1137/24M1690631}
}