Neural fields with random data

Authors

Avitabile D., Cavallini F., Dubinkina S., Lord G. J.

Abstract

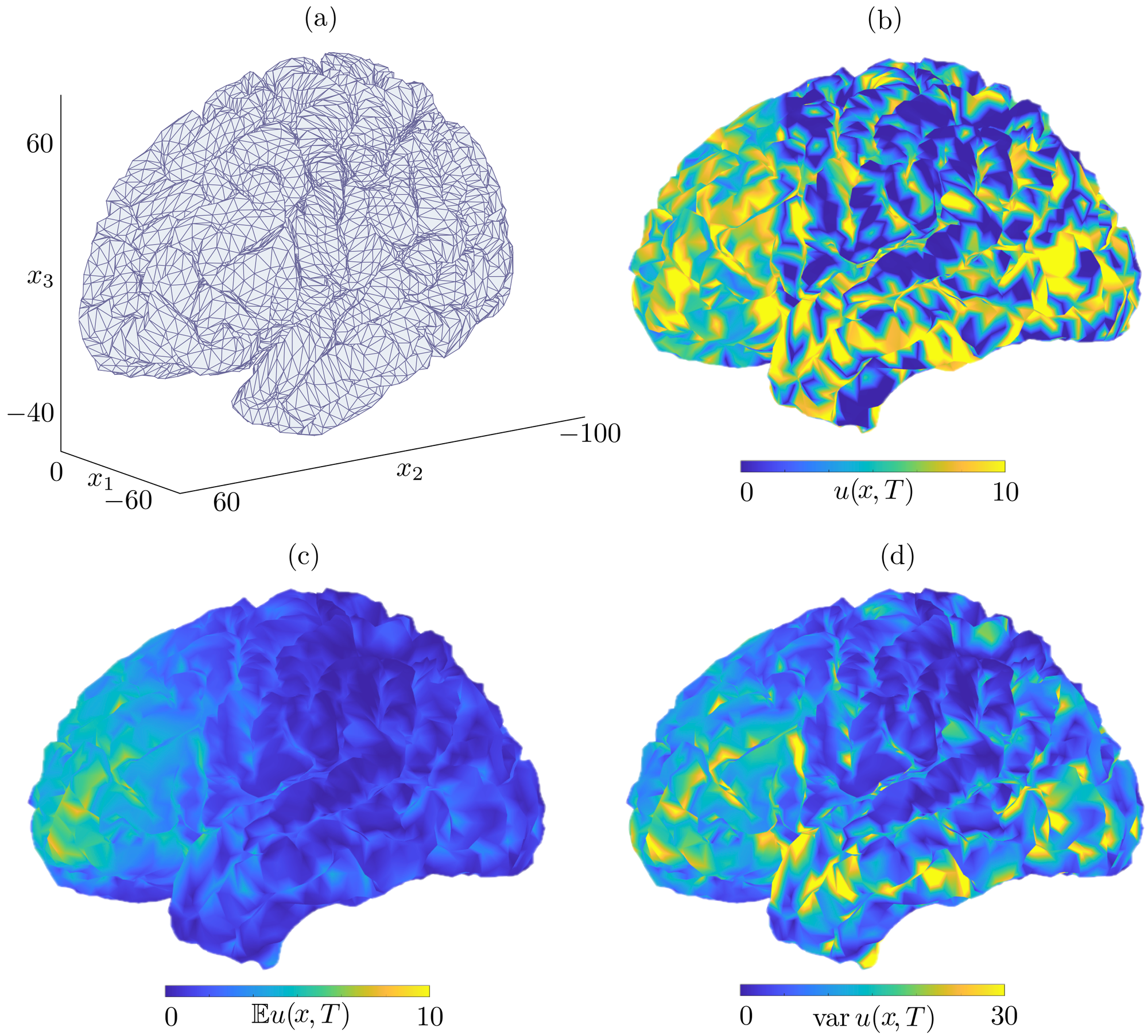
We study neural field equations, which are prototypical models of large-scale cortical activity, subject to random data. We view this spatially-extended, nonlocal evolution equation as a Cauchy problem on abstract Banach spaces, with randomness in the synaptic kernel, firing rate function, external stimuli, and initial conditions. We determine conditions on the random data that guarantee existence, uniqueness, and measurability of the solution in an appropriate Banach space, and examine the regularity of the solution in relation to the regularity of the inputs. We present results for linear and nonlinear neural fields, and for the two most common functional setups in the numerical analysis of this problem. In addition to the continuous problem, we analyse in abstract form neural fields that have been spatially discretised, setting the foundations for analysing uncertainty quantification (UQ) schemes.

Links‌

Arxiv

BibTeX‌

@misc{avitabileNeuralFieldEquations2025,
  title = {Neural {{Field Equations}} with Random Data},
  author = {Avitabile, Daniele and Cavallini, Francesca and Dubinkina, Svetlana and Lord, Gabriel J.},
  year = {2025},
  month = may,
  number = {arXiv:2505.16343},
  eprint = {2505.16343},
  primaryclass = {math},
  publisher = {arXiv},
  doi = {10.48550/arXiv.2505.16343},
  urldate = {2025-05-27},
  archiveprefix = {arXiv},
  langid = {english},
  keywords = {Computer Science - Numerical Analysis,Mathematics - Dynamical Systems,Mathematics - Numerical Analysis,Mathematics - Probability,Nonlinear Sciences - Pattern Formation and Solitons},
}