Quasicrystal patterns in a neural field model

Authors

Gökçe, A., Coombes, S., and Avitabile, D.

Abstract

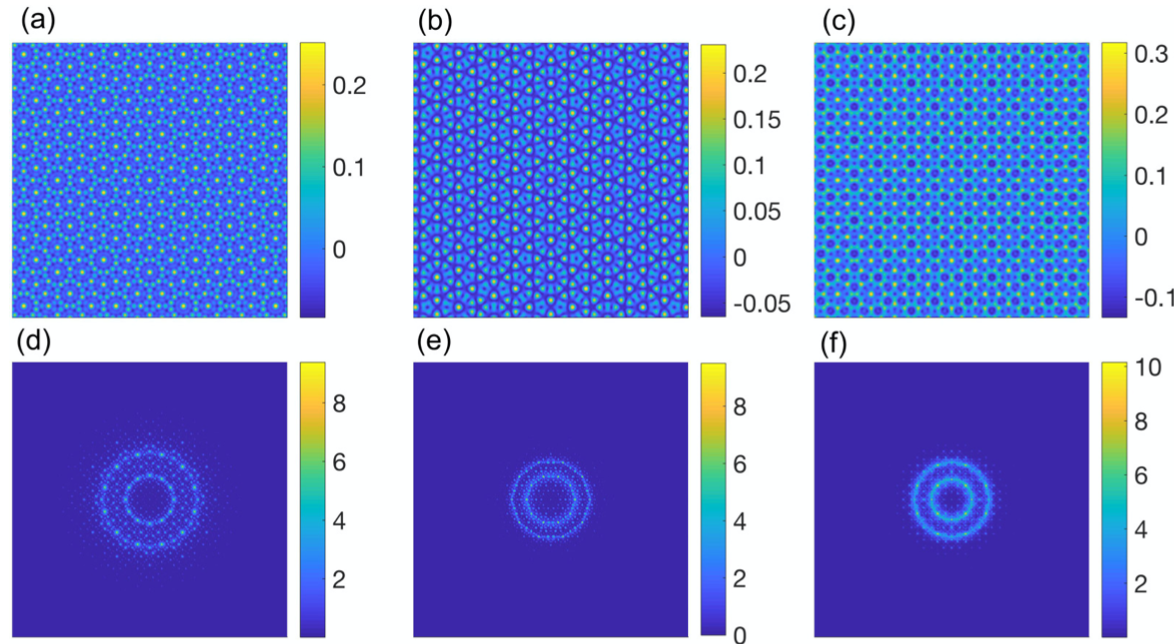
Doubly periodic patterns in planar neural field models have been extensively studied since the 1970s for their role in explaining geometric visual hallucinations. The study of activity patterns that lack translation invariance has received little, if any, attention. Here we show that a scalar neural field model with a translationally invariant kernel can support quasicrystal solutions and that these can be understood using many of the theoretical tools developed previously for materials science. Our approach is constructive in that we consider constraints on the nonlocal kernel describing interactions in the neural field that lead to the simultaneous excitation of two periodic spatial patterns with incommensurate wavelengths. The resulting kernel has a shape that is a modulation of a Mexican-hat kernel. In the neighborhood of the degenerate bifurcation of a homogeneous steady state, we use a Fourier amplitude approach to determine the value of a Lyapunov functional for various periodic and quasicrystal states. For some values of the parameters defining a translationally invariant synaptic kernel of the model, we find that quasicrystal states have the lowest value of the Lyapunov functional. We observe patterns of 12-fold, 10-fold, and 6-fold rotational symmetry that are stable, but none with 8-fold symmetry. We describe some of the visual hallucination patterns that would be perceived from these quasicrystal cortical patterns, making use of the well known inverse retinocortical map from visual neuroscience.

Links

BibTeX

@article{gokce2020quasicrystal,
  title={Quasicrystal patterns in a neural field model},
  author={Gok\c{c}e, Aytul and Coombes, Stephen and Avitabile, Daniele },
  journal={Physical Review Research},
  volume={2},
  issue={1},
  pages={013234},
  numpages = {9},
  year = {2020},
  month = {Mar},
  publisher = {American Physical Society},
  doi = {10.1103/PhysRevResearch.2.013234},
  url = {https://link.aps.org/doi/10.1103/PhysRevResearch.2.013234}
}