Radial Basis Function Techniques for Neural Field Models on Surfaces
Authors
Shaw S. B., Kilpatrick Z. P., Avitabile D.
Abstract
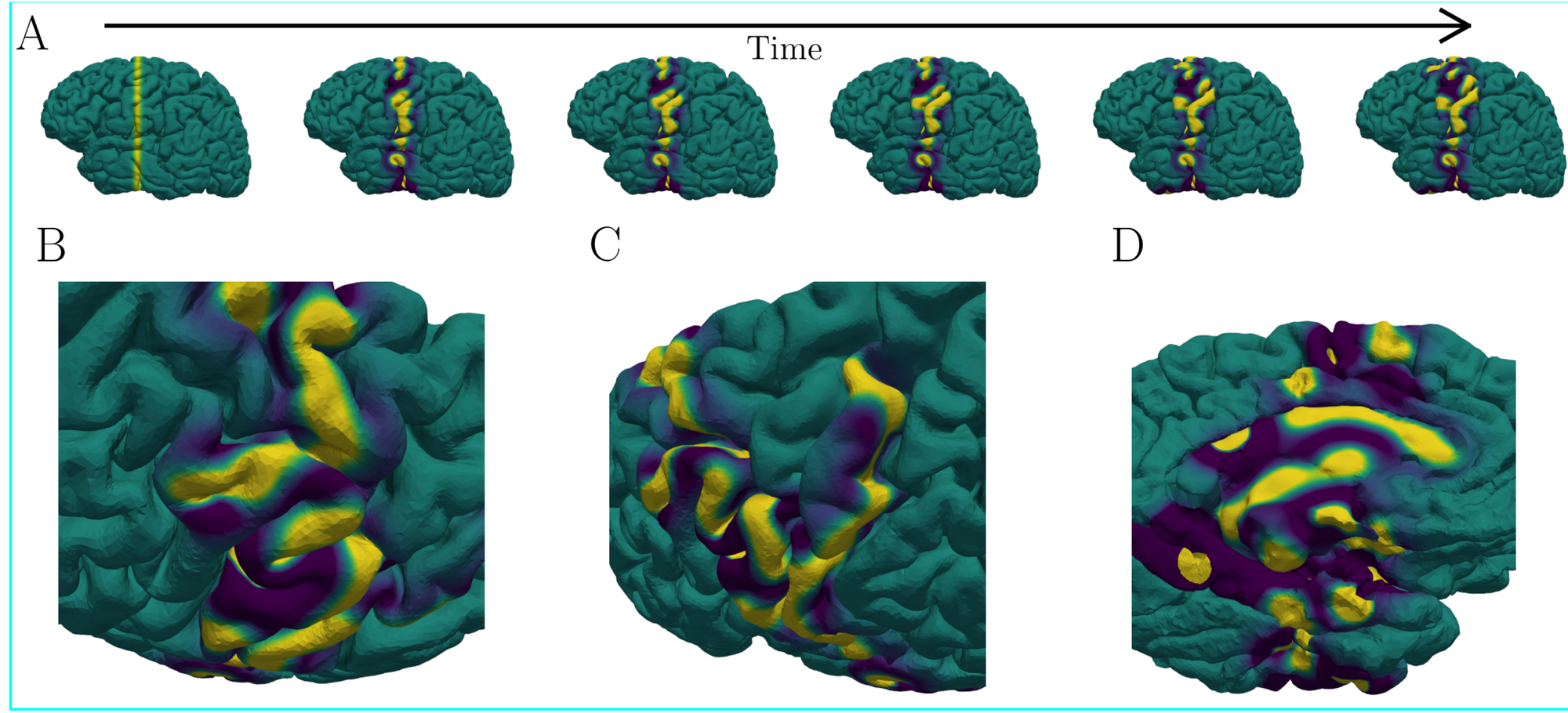
We present a numerical framework for solving neural field equations on surfaces using Radial Basis Function (RBF) interpolation and quadrature. Neural field models describe the evolution of macroscopic brain activity, but modeling studies often overlook the complex geometry of curved cortical domains. Traditional numerical methods, such as finite element or spectral methods, can be computationally expensive and challenging to implement on irregular domains. In contrast, RBF-based methods provide a flexible alternative by offering interpolation and quadrature schemes that efficiently handle arbitrary geometries with high-order accuracy. We first develop an RBF-based interpolatory projection framework for neural field models on general surfaces. Quadrature for both flat and curved domains are derived in detail, ensuring high-order accuracy and stability as they depend on RBF hyperparameters (basis functions, augmenting polynomials, and stencil size). Through numerical experiments, we demonstrate the convergence of our method, highlighting its advantages over traditional approaches in terms of flexibility and accuracy. We conclude with an exposition of numerical simulations of spatiotemporal activity on complex surfaces, illustrating the method's ability to capture complex wave propagation patterns.
Links
ArxivBibTeX
@misc{shawRadialBasisFunction2025,
title = {Radial {{Basis Function Techniques}} for {{Neural Field Models}} on {{Surfaces}}},
author = {Shaw, Sage B. and Kilpatrick, Zachary P. and Avitabile, Daniele},
year = {2025},
month = apr,
number = {arXiv:2504.13379},
eprint = {2504.13379},
primaryclass = {math},
publisher = {arXiv},
doi = {10.48550/arXiv.2504.13379},
urldate = {2025-05-27},
archiveprefix = {arXiv},
langid = {english},
keywords = {Computer Science - Numerical Analysis,Mathematics - Numerical Analysis,Nonlinear Sciences - Pattern Formation and Solitons,Quantitative Biology - Neurons and Cognition},
}