Stochastic collocation schemes for Neural Field Equations with random data

Authors

Avitabile D., Cavallini F., Dubinkina S., Lord G. J.

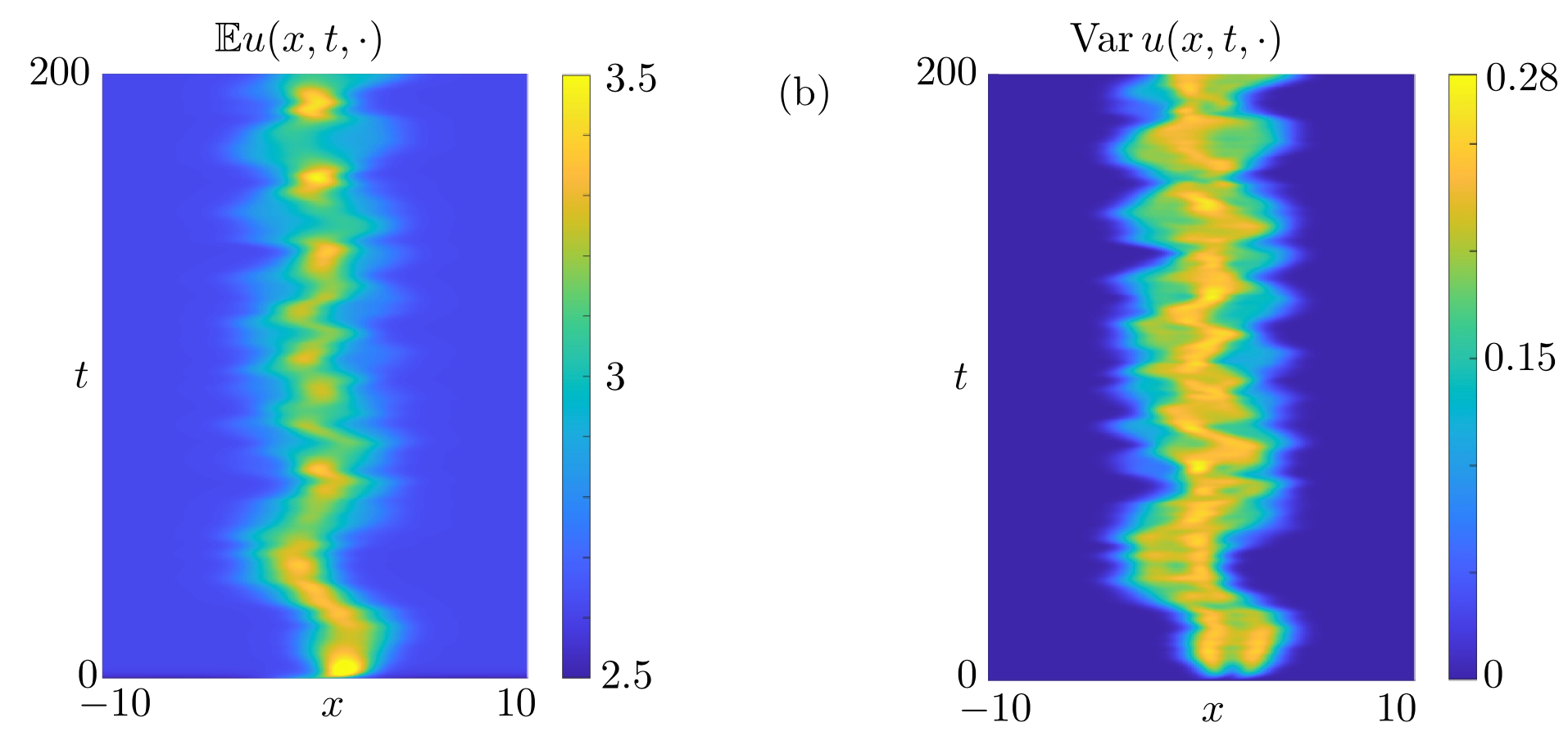
Abstract

We develop and analyse numerical schemes for uncertainty quantification in neural field equations subject to random parametric data in the synaptic kernel, firing rate, external stimulus, and initial conditions. The schemes combine a generic projection method for spatial discretisation to a stochastic collocation scheme for the random variables. We study the problem in operator form, and derive estimates for the total error of the schemes, in terms of the spatial projector. We give conditions on the projected random data which guarantee analyticity of the semi-discrete solution as a Banach-valued function. We illustrate how to verify hypotheses starting from analytic random data and a choice of spatial projection. We provide evidence that the predicted convergence rates are found in various numerical experiments for linear and nonlinear neural field problems.

Links‌

BibTeX‌

@misc{avitabileStochasticCollocationSchemes2025,
  title = {Stochastic Collocation Schemes for {{Neural Field Equations}} with Random Data},
  author = {Avitabile, Daniele and Cavallini, Francesca and Dubinkina, Svetlana and Lord, Gabriel J.},
  year = {2025},
  month = may,
  number = {arXiv:2505.16443},
  eprint = {2505.16443},
  primaryclass = {math},
  publisher = {arXiv},
  doi = {10.48550/arXiv.2505.16443},
  urldate = {2025-05-27},
  archiveprefix = {arXiv},
  langid = {english},
  keywords = {Computer Science - Numerical Analysis,Mathematics - Dynamical Systems,Mathematics - Numerical Analysis,Nonlinear Sciences - Pattern Formation and Solitons},
}