Stripe to spot transition in a plant root hair initiation model

Authors

Bren͂a-Medina, V.F., Avitabile, D., Champneys, A.R. and Ward, M.J.

Abstract

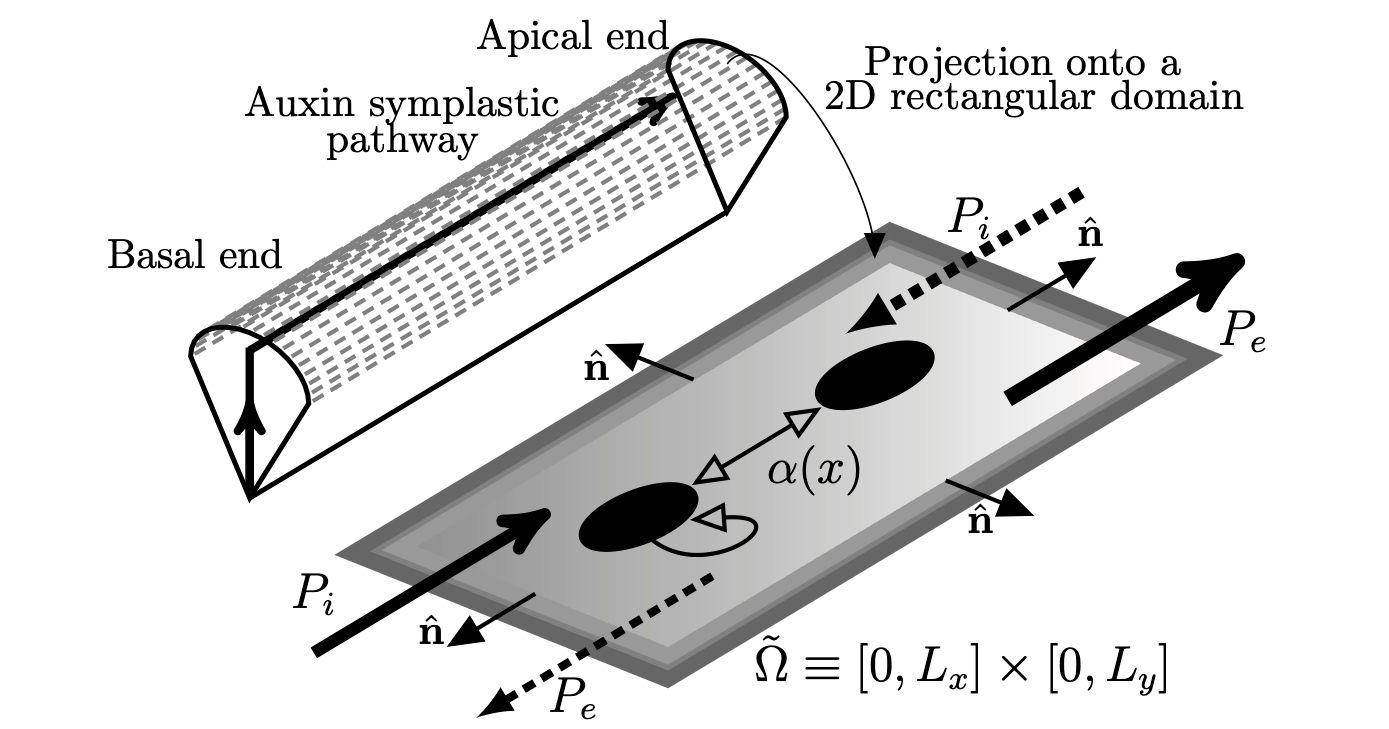
A generalized Schnakenberg reaction-diffusion system with source and loss terms and a spatially dependent coefficient of the nonlinear term is studied both numerically and analytically in two spatial dimensions. The system has been proposed as a model of hair initiation in the epidermal cells of plant roots. Specifically the model captures the kinetics of a small G-protein ROP, which can occur in active and inactive forms, and whose activation is believed to be mediated by a gradient of the plant hormone auxin. Here the model is made more realistic with the inclusion of a transverse coordinate. Localized stripe-like solutions of active ROP occur for high enough total auxin concentration and lie on a complex bifurcation diagram of single- and multipulse solutions. Transverse stability computations, confirmed by numerical simulation show that, apart from a boundary stripe, these one-dimensional (1D) solutions typically undergo a transverse instability into spots. The spots so formed typically drift and undergo secondary instabilities such as spot replication. A novel two-dimensional (2D) numerical continuation analysis is performed that shows that the various stable hybrid spot-like states can coexist. The parameter values studied lead to a natural, singularly perturbed, so-called semistrong interaction regime. This scaling enables an analytical explanation of the initial instability by describing the dispersion relation of a certain nonlocal eigenvalue problem. The analytical results are found to agree favorably with the numerics. Possible biological implications of the results are discussed.

Links

BibTeX

@article{bren͂a2015stripe,
  title={Stripe to spot transition in a plant root hair initiation model},
  author={Bren͂a--Medina, Victor F and Avitabile, Daniele and Champneys, Alan R and Ward, Michael J},
  journal={SIAM Journal on Applied Mathematics},
  volume={75},
  number={3},
  pages={1090--1119},
  year={2015},
  publisher={SIAM}
}