The dynamics of neural fields on bounded domains: an interface approach for dirichlet boundary conditions

Authors

Gökçe, A., Avitabile, D. and Coombes, S.

Abstract

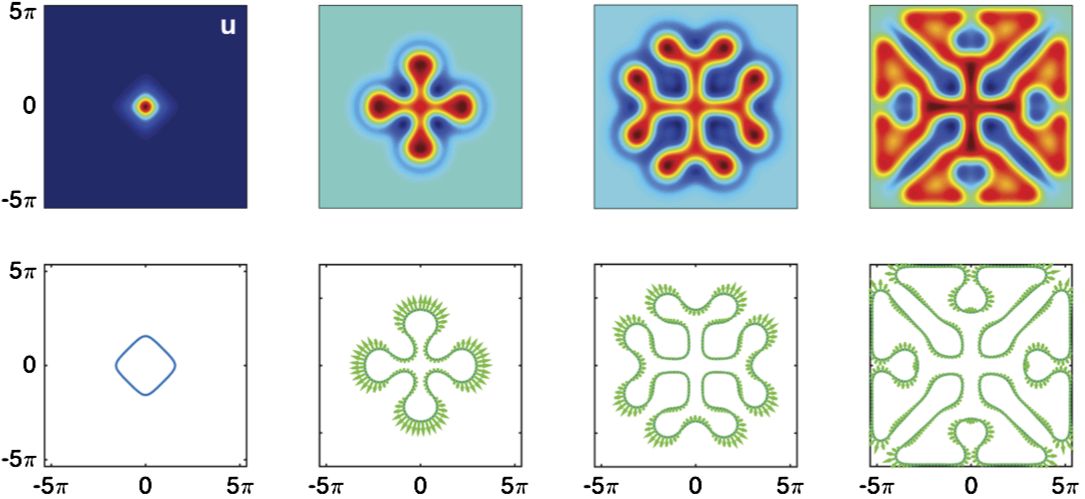
Continuum neural field equations model the large-scale spatio-temporal dynamics of interacting neurons on a cortical surface. They have been extensively studied, both analytically and numerically, on bounded as well as unbounded domains. Neural field models do not require the specification of boundary conditions. Relatively little attention has been paid to the imposition of neural activity on the boundary, or to its role in inducing patterned states. Here we redress this imbalance by studying neural field models of Amari type (posed on one- and two-dimensional bounded domains) with Dirichlet boundary conditions. The Amari model has a Heaviside nonlinearity that allows for a description of localised solutions of the neural field with an interface dynamics. We show how to generalise this reduced but exact description by deriving a normal velocity rule for an interface that encapsulates boundary effects. The linear stability analysis of localised states in the interface dynamics is used to understand how spatially extended patterns may develop in the absence and presence of boundary conditions. Theoretical results for pattern formation are shown to be in excellent agreement with simulations of the full neural field model. Furthermore, a numerical scheme for the interface dynamics is introduced and used to probe the way in which a Dirichlet boundary condition can limit the growth of labyrinthine structures.

Links

BibTeX

@article{gokcce2017dynamics,
  title={The dynamics of neural fields on bounded domains: an interface approach for dirichlet boundary conditions},
  author={G{\"o}k{\c{c}}e, Ayt{\"u}l and Avitabile, Daniele and Coombes, Stephen},
  journal={The Journal of Mathematical Neuroscience},
  volume={7},
  number={1},
  pages={12},
  year={2017},
  publisher={Springer}
}