To snake or not to snake in the planar Swift–Hohenberg equation
Authors
Avitabile, D., Lloyd, D.J., Burke, J., Knobloch, E. and Sandstede, B.
Abstract
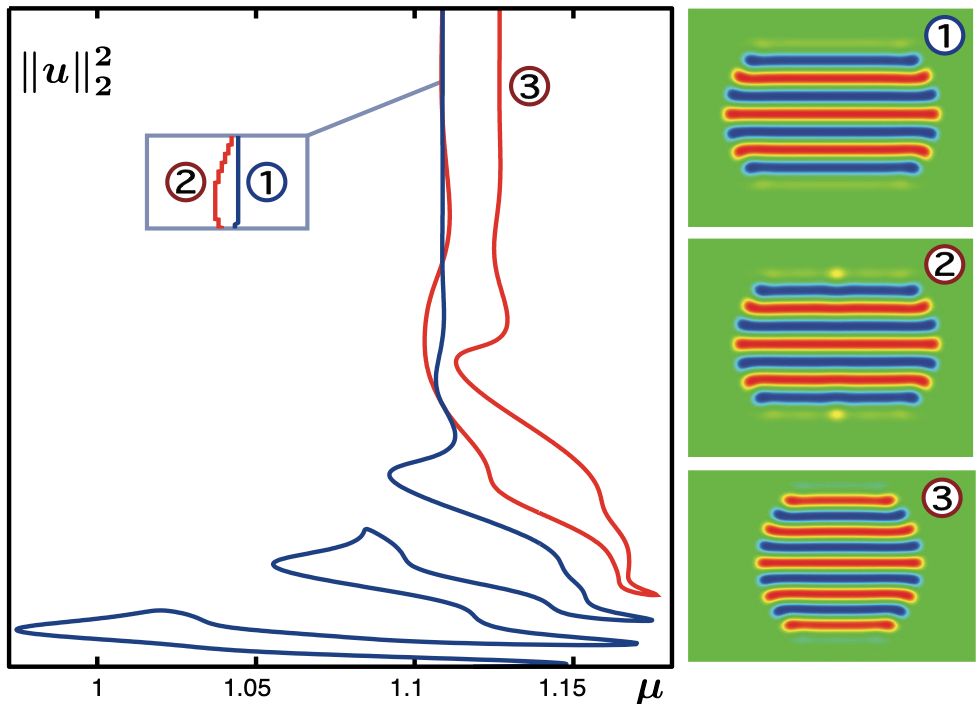
We investigate the bifurcation structure of stationary localized patterns of the two-dimensional Swift–Hohenberg equation on an infinitely long cylinder and on the plane. On cylinders, we find localized roll, square, and stripe patches that exhibit snaking and nonsnaking behavior on the same bifurcation branch. Some of these patterns snake between four saddle-node limits; in this case, recent analytical results predict the existence of a rich bifurcation structure to asymmetric solutions, and we trace out these branches and the PDE spectra along these branches. On the plane, we study the bifurcation structure of fully localized roll structures, which are often referred to as worms. In all the above cases, we use geometric ideas and spatial-dynamics techniques to explain the phenomena that we encounter.
Links
DOI PDFBibTeX
@article{avitabile2010snake,
title={To snake or not to snake in the planar Swift--Hohenberg equation},
author={Avitabile, Daniele and Lloyd, David JB and Burke, John and Knobloch, Edgar and Sandstede, Bj{\"o}rn},
journal={SIAM Journal on Applied Dynamical Systems},
volume={9},
number={3},
pages={704--733},
year={2010},
publisher={SIAM}
}